グラフ 連結成分 アルゴリズム
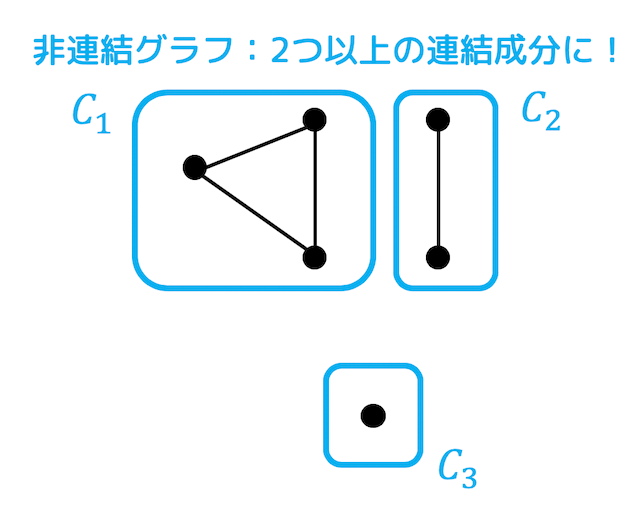
非連結グラフは いくつかの連結部分グラフのグループに分割することができます この連結部分グラフのことを 連結成分 と呼びます 先ほどの例でいうと下のように3つの連結成分に分けることができ. アルゴリズムIⅠB 第2回 強連結成分最小全域木 392 強連結成分 深さ優先探索の古典的な応用有向グラフを強連結成分に分 割 有向グラフGVEの強連結成分とはCのすべての頂点対 uvに対してuとvがお互いに到達可能な頂点の極大集合C𝑉.

Flink達成詳細connectedcomponents接続されたコンポーネント 増分反復アルゴリズム デルタ反復 を達成 コードワールド

強連結成分 Scc Technical Note
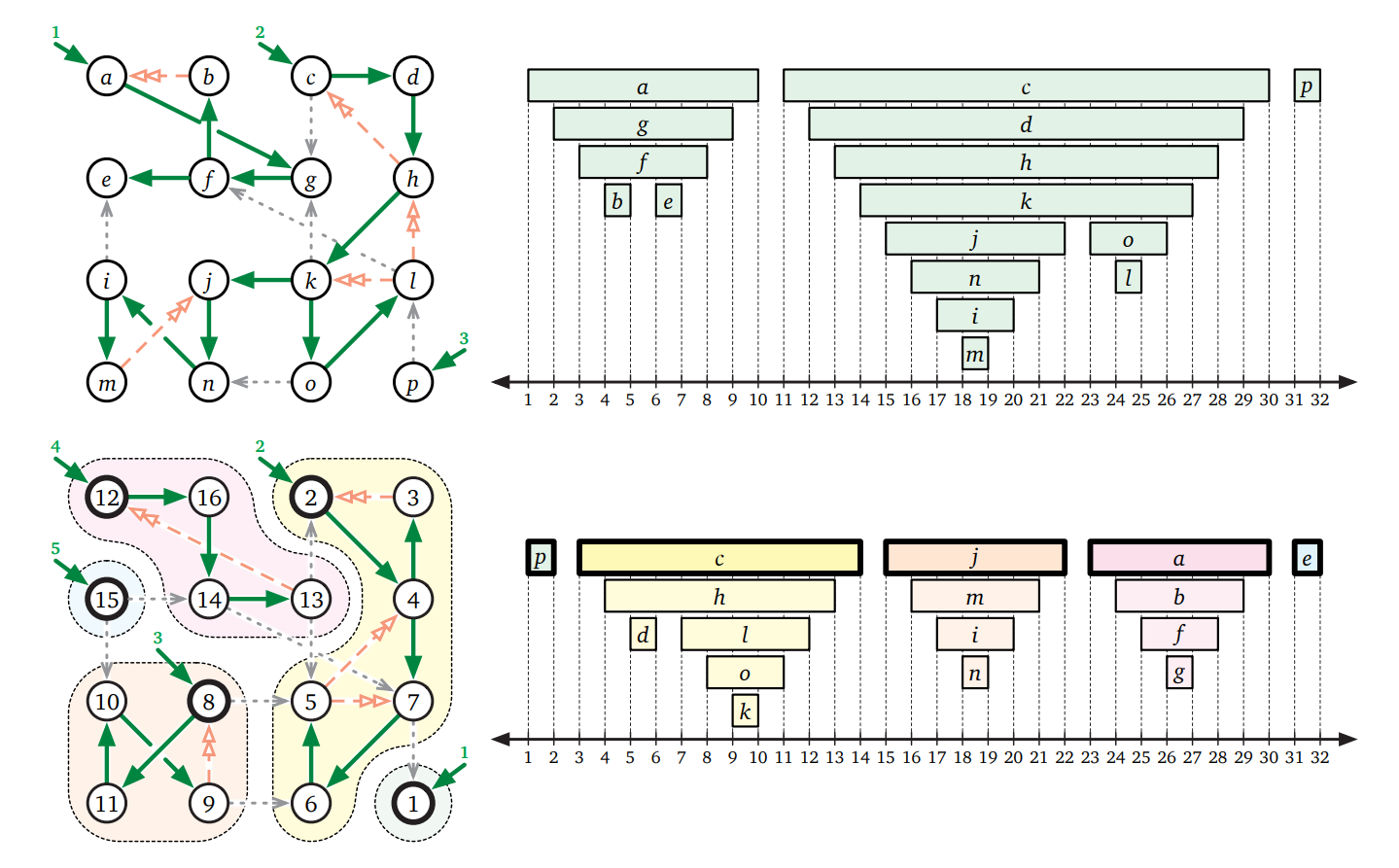
線形時間で強連結成分を求める 深さ優先探索 アルゴリズム 翻訳
連結グラフと連結成分について簡単にまとめてから問題を解いていきます 連結グラフ グラフに含まれる全ての頂点が他のいずれかの頂点とリンクしているようなグラフを連結グラフと言いますこんな感じ 連結成分 あるグラフの部分グラフのうち極大で連結なものを連結成分と呼び.

グラフ 連結成分 アルゴリズム. 適当な頂点から深さ優先探索を行うその際各頂点 v v v に対して頂点 v v v から進めなくなった順番 t v tv t v を格納する. 無向グラフの2連結成分 無向グラフGV Eにおいて 頂点u v は同じ2連結成分に含まれる u v 以外の頂点w を削除しても uからvへの路が存在 a d c e g f h b k j l i a とk は同じ 2連結成分に含まれない b を削除すると a からk への 路が存在しない b とg は同じ 2. グラフGV E を表現するデータ構造 接続行列--- 領域計算量Omn 隣接行列--- 領域計算量On2 2次元配列を使う 実現は簡単 疎なグラフに対して無駄が多い 隣接リスト--- 領域計算量Omn 複数の連結リストを使う 実現は少し複雑 どのグラフに対しても無駄がない.
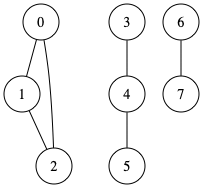
グラフ𝐺に対する全域木spanning tree アルゴリズムとデータ構造13 7 無向グラフ𝐺1𝑉1𝐸1 𝐺2𝑉2𝐸2 定義𝐺1が𝐺2の全域木スパニング木 である 𝐺1は𝐺2の全頂点を含む部分グラフで木である 𝑉1𝑉2かつ𝐸1𝐸2 𝐺1 𝐺1 𝐺2 𝐺1は𝐺2の全域木である. はじめに 今回はグラフの連結成分を調べるアルゴリズムを実装してみようと思いますそもそもグラフの連結成分とは任意の2点間に道があるグラフのうち極大な連結部分グラフのことをいいます以下の画像のようなグラフだと0 12 3 45 6 7の3つの連結成分があることになり. 連結成分とは任意の2頂点間にパスが存在するような部分グラフのうち極大なもののことを言います 連結成分は3つ アルゴリズム グラフ gve の連結成分の個数を数えるアルゴリズム 未探索の頂点について以下を行うdfs or bfs で同じ連結成分に含まれる頂点を全て探索済み.
図445 強連結グラフ 図446 強連結成分への分割 強連結 255ページ 有向グラフの各頂点から任意の 頂点へ至る道が存在するとき この有向グラフを強連結であるという 部分グラフのうち強連結で. 連結成分connected component アルゴリズムとデータ構造12 無向グラフ𝐺𝑉𝐸 𝐺を連結成分𝐺1𝑉1𝐸1 𝐺 𝑉 𝐸 に分割する 2つの頂点 が同じ連結成分に属す を結ぶパスが存在 連結成分は4 個 連結成分は1 個. 深さ優先探索dfs でグラフをたどる dfs 木の葉に近いものから順に関節点を見付け 毎回その関節点を含む一つの2連結成分を出力 関節点.
グラフの用語 連結成分 から へのパスも から へのパスも存在-するときに と が同じグループに属する とし て 𝑉 をグループ分けしたときの各グループを連 結成分 connected component という 有向グラフでは強連結成分 strongly connected. はじめに 今回は最小頂点被覆問題の近似アルゴリズムを実装してみたいと思います最小頂点被覆問題の詳細は後述しますがnp困難の問題と知られていて多項式時間で解くことできないことが証明されていますそういった解くことが難しい問題に関して以下の3つの手段を検討しながら. 連結成分とは任意の2頂点間にパスが存在するような部分グラフのうち極大なもののことを言います グラフ GVE 上の2頂点 uv が同じ連結成分に属しているか判定するアルゴリズムについてです 頂点0と頂点2は同じ連結成分頂点1と頂点4 は違う連結成分 アルゴリズム 単純な.
グラフの強連結成分分解1 基礎数理 1 簡単な例題 図1のグラフが何らかのシステムの状態推移を表していると考えようシステムには六 つの状態fv1v2v3v4v5v6g があり辺vivjがあるときには状態vi から状態vj に変 化する可能性があるこのグラフから次のようなことがわかる.
連結グラフと連結成分 プログラミング原人の進化論
有向グラフを強連結成分に分解するアルゴリズム さすらうプログラマの日記
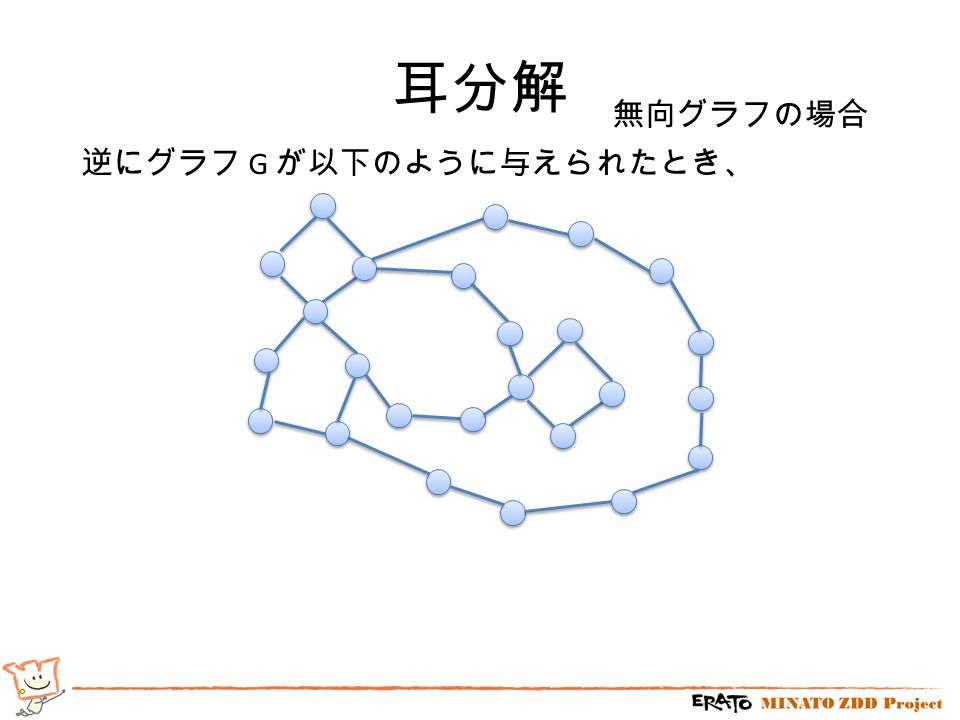
組合せ最適化輪講 2 3 連結性 川原 純 2 3 連結性 内容 グラフ上の節点をすべてたどるアルゴリズム 計算機上でのグラフの表現 強 連結成分を求めるアルゴリズム トポロジカル順序を求める方法も K 連結 K 辺連結について 2 連結グラフの耳分解について
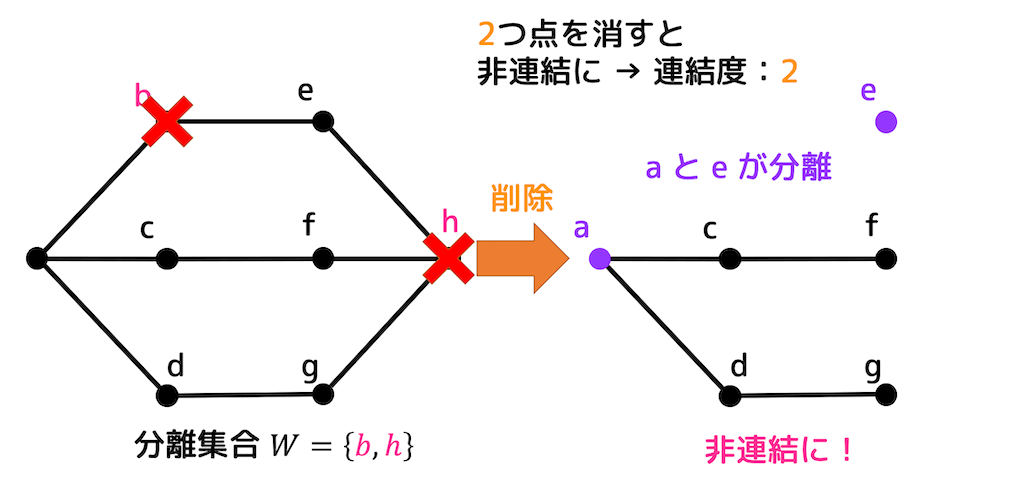
うさぎでもわかる離散数学 グラフ理論 第16羽 グラフの連結性 連結度 工業大学生ももやまのうさぎ塾

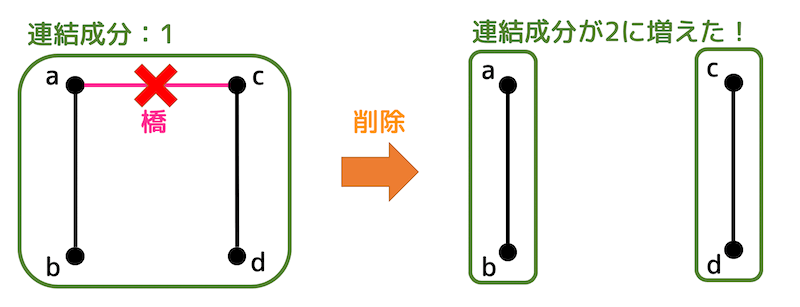
橋 二重辺連結成分分解 あったこといろいろ
うさぎでもわかる離散数学 グラフ理論 第9羽 グラフの基礎3 工業大学生ももやまのうさぎ塾
うさぎでもわかる離散数学 グラフ理論 第9羽 グラフの基礎3 工業大学生ももやまのうさぎ塾
グラフの連結成分の個数を求めるアルゴリズム アルゴリズムロジック
You have just read the article entitled グラフ 連結成分 アルゴリズム. You can also bookmark this page with the URL : https://laborersuppo.blogspot.com/2022/11/blog-post_958.html
0 Response to "グラフ 連結成分 アルゴリズム"
Post a Comment